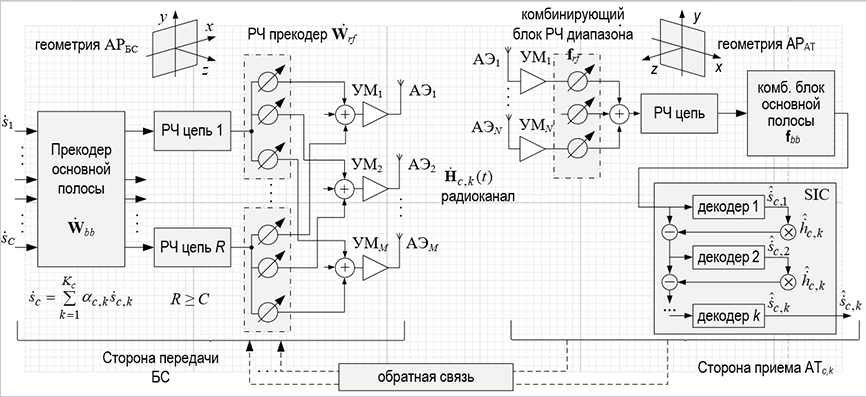
Mathematical Model of the MIMO-NOMA System

Relevance of the Study. Modern next-generation mobile networks impose extremely high requirements on spectral efficiency, reliability, and robustness in urban environments with high user density. The MIMO-NOMA technology, despite its proven potential, requires a revision of existing models due to the need to account for users' spatial dynamics, polarization distortions, hardware nonlinearity, and channel state information (CSI) estimation errors. The lack of comprehensive models capable of simultaneously addressing these factors significantly limits the ability to effectively optimize systems in practical scenarios.

Research Objective. The study aims to develop a comprehensive mathematical model of the MIMO-NOMA segment between the precoder and the summation scheme in the complex baseband domain, accounting for terminal mobility and orientation, antenna polarization, amplifier nonlinearities, and CSI errors, to analyze and optimize precoding and successive interference cancellation (SIC) algorithms.

Research Methods. The modeling incorporates: stochastic processes (including the Ornstein–Uhlenbeck model and social force models) to describe user mobility; analytical geometry to represent the spatial orientation of antennas; electromagnetic propagation theory methods to model cross-polarization effects; and Saleh and Volterra models to describe power amplifier nonlinearities in the FR1 and FR2 frequency ranges.

Research Results. A vector signal model was derived, incorporating the effects of terminal orientation, interference, polarization and nonlinear distortions, and CSI errors. Analytical expressions were obtained for evaluating SINR, SER, throughput, and energy efficiency, considering all distortions. A comparative analysis of the proposed model against existing standards (3GPP, ITU-R) and academic approaches (DL-based, IRS-assisted) demonstrated its superiority in terms of realism and analytical completeness.

Scientific Novelty. For the first time, a mathematical model of the MIMO-NOMA system is proposed that simultaneously accounts for terminal dynamics, dual polarization, nonlinearities with memory effects, and multipath scenarios, providing an analytical description within a unified parameter space.

Theoretical and Practical Significance. The model refines the description of the MIMO-NOMA channel and supports the optimization of precoders, summation schemes in the complex baseband domain, and SIC algorithms in next-generation mobile networks, particularly in conditions of high mobility and dense urban environments.

1. Ding Z., Lei X., Karagiannidis G.K., Schober R., Yuan J., Bhargava V.K. A Survey on Non-Orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends. IEEE Journal on Selected Areas in Communications. 2017;35(10):2181–2195. DOI:10.1109/JSAC.2017.2725519. EDN:YGQORJ

2. Willems J., Corbetta A., Menkovski V., Toschi F. Pedestrian orientation dynamics from high-fidelity measurements. Scientific Reports. 2020;10(1):11653. DOI:10.1038/s41598-020-68287-6

3. Helbing D., Molnar P. Social Force Model for Pedestrian Dynamics. Physical Review E. 1998;51(5):482–486. DOI:10.1103/PhysRevE.51.4282

4. Ge Q., Sun Q., Li S.E., Zheng S., Wu W., Chen X. Numerically Stable Dynamic Bicycle Model for Discrete-Time Control. Proceedings of the Intelligent Vehicles Symposium Workshops, IV Workshops, 11–17 July 2021, Nagoya, Japan. IEEE; 2021. p.128–134. DOI:10.1109/IVWorkshops54471.2021.9669260

5. Lai F., Huang C. Seventh-Degree Polynomial-Based Single Lane Change Trajectory Planning and Four-Wheel Steering Model Predictive Tracking Control for Intelligent Vehicles. Vehicles. 2024;6(4):2228–2250. DOI:10.3390/vehicles6040109. EDN:MERHQF

6. Rec. ITU-R P.1411-12 (08/2023). Propagation data and prediction methods for the planning of short-range outdoor radiocommunication systems and radio local area networks in the frequency range 300 MHz to 100 GHz.

7. 3GPP TR 38.901 V18.0.0 (2023-12). Study on Channel Model for Frequencies from 0.5 to 100 GHz.

8. Rec. ITU-R P.530-18 (09/2021). Propagation data and prediction methods required for the design of terrestrial line-of-sight systems.

9. Rec. ITU-R P.833-10 (09/2021). Attenuation in vegetation.

10. Rec. ITU-R P.838-3 (1992-1999-2003-2005). Specific attenuation model for rain for use in prediction methods.

11. Molisch A. F. Wireless Communications. John Wiley & Sons; 2011. 884 p.

12. Ma Z., Ai B., He R., Wang G., Zhong Z., Yang M. Impact of UAV Rotation on MIMO Channel Space-Time Correlation. Proceedings of the 92nd Vehicular Technology Conference, VTC2020-Fall, 18 November 2020 – 16 December 2020, Victoria, Canada. IEEE; 2021. DOI:10.1109/VTC2020-Fall49728.2020.9348811

13. Zeng L., Cheng X., Wang C.-X., Yin X. A 3D Geometry-Based Stochastic Channel Model for UAV-MIMO Channels. Proceedings of the Wireless Communications and Networking Conference, WCNC, 19–22 March 2017, San Francisco, USA. IEEE; 2017. DOI:10.1109/WCNC.2017.7925794

14. Wu Y., Gu Y., Wang Z. Efficient Channel Estimation for mmWave MIMO With Transceiver Hardware Impairments. IEEE Transactions on Vehicular Technology. 2019;68(10):9883–9895. DOI:10.1109/TVT.2019.2934167

15. Beddiaf S., Khelil A., Khennoufa F., Kara F., Kaya H., Li X. A Unified Performance Analysis of Cooperative NOMA with Prac-tical Constraints: Hardware Impairment, Imperfect SIC and CSI. IEEE Access. 2022;10:132931–132948. DOI:10.1109/access.2022.3230650. EDN:EIBYDD

16. Saleh A.A.M. Frequency-Independent and Frequency-Dependent Nonlinear Models of TWT Amplifiers. IEEE Transactions on Communications. 1981;29(11):1715–1720. DOI:10.1109/TCOM.1981.1094911

17. Isaksson M., Wisell D., Ronnow D. A comparative analysis of behavioral models for RF power amplifiers. IEEE Transactions on Microwave Theory and Techniques. 2006;54(1):348–359. DOI:10.1109/TMTT.2005.860500

18. Rönnow D. Software for determining the third order Volterra kernels of radio frequency power amplifiers. 2005. DOI:10.13140/2.1.4327.8724

19. Sinilnikov A.M., Fokin G.A., Grishin I.V., Kalinkina A.A. Throughput Analysis of MIMO-NOMA Systems. Elektrosvyaz. 2024; 10:20–32. (in Russ.) DOI:10.34832/ELSV.2024.59.10.004. EDN:DFCTXZ

20. Sinilnikov A.M., Fokin G.A., Grishin I.V., Kalinkina A.A. Analysis of power-division non-orthogonal multiple access technology. The Herald of the Siberian State University of Telecommunications and Information Science. 2024;18(4):3–21. (in Russ.) DOI:10.55648/1998-6920-2024-18-4-3-21. EDN:HOVCSL

21. Jain R., Chiu D.-M., Hawe W.R. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems. DEC Research Report TR-301. 1984.

22. Rec. ITU-R M.2412-0 (10/2017). Guidelines for evaluation of radio interface technologies for IMT 2020.

23. Kyösti P., Meinilä J., Hentilä L., Holma P., Käske M., Narandžić M., et al. WINNER II Channel Models for System Level Simulations. Final Report on Model Specification. Version 1.2. 2008. URL: http://signserv.signal.uu.se/Publications/WINNER/WIN2D112.pdf

24. Holma P., Meinilä J., Kyösti P., Hentilä L., Jämsä T., Suikkanen E., et al. CP5-026 WINNER+ D5.3 v1.0 WINNER+ Final Channel Models. 2010.

25. Chi Y., Liu L., Song G., Yuen C., Guan Y.L., Li Y. Practical MIMO-NOMA: Low Complexity & Capacity-Approaching Solution. arXiv preprint. 2018. DOI:10.48550/arXiv.1807.06846

26. de Sena A.S., Nardelli P.H.J., da Costa D.B., Lima F.R.M., Yang L., Popovski P., Ding Z., Papadias C.B. IRS-Assisted Massive MIMO-NOMA Networks with Polarization Diversity. arXiv preprint. 2021. DOI:10.48550/arXiv.2105.12952