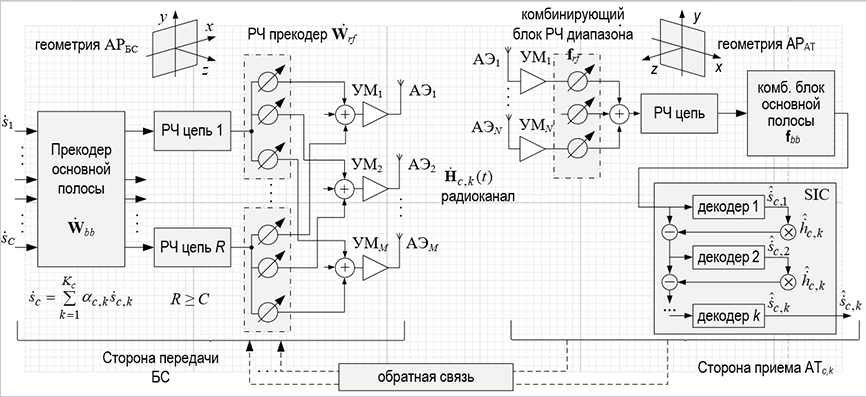
Математическая модель системы MIMO-NOMA

Актуальность исследования. Современные сети мобильной связи нового поколения предъявляют крайне высокие требования к спектральной эффективности, надежности и устойчивости работы в условиях городской застройки и высокой плотности пользователей. Технология MIMO-NOMA, несмотря на доказанный потенциал, требует пересмотра существующих моделей в связи с необходимостью учета пространственной динамики пользователей, поляризационных искажений, аппаратной нелинейности и ошибок оценки канала. Отсутствие комплексных моделей, способных учесть эти факторы одновременно, значительно ограничивает возможность адекватной оптимизации систем в практических сценариях.

Целью исследования является построение полной математической модели участка MIMO-NOMA между прекодером и схемой сложения в комплексной низкочастотной области, учитывающей движение и ориентацию терминалов, поляризацию антенн, нелинейности усилителей и ошибки CSI для анализа и оптимизации алгоритмов прекодирования и SIC.

Методы исследования. В рамках моделирования применены: стохастические процессы (включая модель Орнштейна – Уленбека и социальные силы) для описания движения пользователей; аналитическая геометрия для описания пространственной ориентации антенн; методы теории электромагнитного распространения для моделирования кросс-поляризационных эффектов; модели Салеха и Вольтерра для описания нелинейности усилителей мощности в диапазонах FR1 и FR2.

Результаты исследования. Получена векторная модель сигнала, учитывающая влияние ориентации терминала, интерференции, поляризационных и нелинейных искажений, а также ошибок CSI. Выведены аналитические выражения для оценки SINR, SER, пропускной способности и энергетической эффективности с учетом всех искажений. Проведен сравнительный анализ предложенной модели с существующими стандартами (3GPP, ITU-R) и академическими подходами (DL-based, IRS-assisted), показавший ее преимущество по степени реализма и аналитической полноте.

Научная новизна. Впервые предложена математическая модель системы MIMO-NOMA, одновременно учитывающая динамику терминалов, двойную поляризацию, нелинейности с эффектами памяти и многолучевые сценарии, обеспечивая аналитическое описание в едином пространстве параметров.

Теоретическая и практическая значимость. Модель уточняет описание канала MIMO-NOMA и поддерживает оптимизацию прекодеров, схем сложения в комплексной низкочастотной области и алгоритмов SIC в сетях мобильной связи нового поколения, особенно в условиях высокой подвижности и плотной городской застройки.

1. Ding Z., Lei X., Karagiannidis G.K., Schober R., Yuan J., Bhargava V.K. A Survey on Non-Orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends // IEEE Journal on Selected Areas in Communications. 2017. Vol. 35. Iss. 10. PP. 2181–2195. DOI:10.1109/JSAC.2017.2725519. EDN:YGQORJ

2. Willems J., Corbetta A., Menkovski V., Toschi F. Pedestrian orientation dynamics from high-fidelity measurements // Scientific Reports. 2020. Vol. 10. Iss. 1. PP. 11653. DOI:10.1038/s41598-020-68287-6

3. Helbing D., Molnar P. Social Force Model for Pedestrian Dynamics // Physical Review E. 1998. Vol. 51. Iss. 5. PP. 482–486. DOI:10.1103/PhysRevE.51.4282

4. Ge Q., Sun Q., Li S.E., Zheng S., Wu W., Chen X. Numerically Stable Dynamic Bicycle Model for Discrete-Time Control // Proceedings of the Intelligent Vehicles Symposium Workshops (IV Workshops, Nagoya, Japan, 11–17 July 2021). IEEE, 2021. PP. 128–134. DOI:10.1109/IVWorkshops54471.2021.9669260

5. Lai F., Huang C. Seventh-Degree Polynomial-Based Single Lane Change Trajectory Planning and Four-Wheel Steering Model Predictive Tracking Control for Intelligent Vehicles // Vehicles. 2024. Vol. 6. Iss. 4. PP. 2228–2250. DOI:10.3390/vehicles6040109. EDN:MERHQF

6. Rec. ITU-R P.1411-12 (08/2023). Propagation data and prediction methods for the planning of short-range outdoor radio-communication systems and radio local area networks in the frequency range 300 MHz to 100 GHz.

7. 3GPP TR 38.901 V18.0.0 (2023-12). Study on Channel Model for Frequencies from 0.5 to 100 GHz.

8. Rec. ITU-R P.530-18 (09/2021). Propagation data and prediction methods required for the design of terrestrial line-of-sight systems.

9. Rec. ITU-R P.833-10 (09/2021). Attenuation in vegetation.

10. Rec. ITU-R P.838-3 (1992-1999-2003-2005). Specific attenuation model for rain for use in prediction methods.

11. Molisch A.F. Wireless Communications. John Wiley & Sons, 2011. 884 p.

12. Ma Z., Ai B., He R., Wang G., Zhong Z., Yang M. Impact of UAV Rotation on MIMO Channel Space-Time Correlation // Proceedings of the 92nd Vehicular Technology Conference (VTC2020-Fall, Victoria, Canada, 18 November 2020 – 16 December 2020). IEEE, 2021. DOI:10.1109/VTC2020-Fall49728.2020.9348811

13. Zeng L., Cheng X., Wang C.-X., Yin X. A 3D Geometry-Based Stochastic Channel Model for UAV-MIMO Channels // Proceedings of the Wireless Communications and Networking Conference (WCNC, San Francisco, USA, 19–22 March 2017). IEEE, 2017. DOI:10.1109/WCNC.2017.7925794

14. Wu Y., Gu Y., Wang Z. Efficient Channel Estimation for mmWave MIMO With Transceiver Hardware Impairments // IEEE Transactions on Vehicular Technology. 2019. Vol. 68. Iss. 10. PP. 9883–9895. DOI:10.1109/TVT.2019.2934167

15. Beddiaf S., Khelil A., Khennoufa F., Kara F., Kaya H., Li X. A Unified Performance Analysis of Cooperative NOMA with Prac-tical Constraints: Hardware Impairment, Imperfect SIC and CSI // IEEE Access. 2022. Vol. 10. PP. 132931–132948. DOI:10.1109/access.2022.3230650. EDN:EIBYDD

16. Saleh A.A.M. Frequency-Independent and Frequency-Dependent Nonlinear Models of TWT Amplifiers // IEEE Transactions on Communications. 1981. Vol. 29. Iss. 11. PP. 1715–1720. DOI:10.1109/TCOM.1981.1094911

17. Isaksson M., Wisell D., Ronnow D. A comparative analysis of behavioral models for RF power amplifiers // IEEE Transactions on Microwave Theory and Techniques. 2006. Vol. 54. Iss. 1. PP. 348–359. DOI:10.1109/TMTT.2005.860500

18. Rönnow D. Software for determining the third order Volterra kernels of radio frequency power amplifiers. 2005. DOI:10.13140/2.1.4327.8724

19. Синильников А.М., Фокин Г.А., Гришин И.В., Калинкина А.А. Анализ пропускной способности систем MIMO-NOMA // Электросвязь. 2024. № 10. С. 20–32. DOI:10.34832/ELSV.2024.59.10.004. EDN:DFCTXZ

20. Синильников А.М., Фокин Г.А., Гришин И.В., Калинкина А.А. Анализ технологии неортогонального множественного доступа с разделением по мощности PD-NOMA // Вестник СибГУТИ. 2024. Т. 18. №. 4. С. 3–21. DOI:10.55648/1998-6920-2024-18-4-3-21. EDN:HOVCSL

21. Jain R., Chiu D.-M., Hawe W.R. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems. DEC Research Report TR-301. 1984.

22. Rec. ITU-R M.2412-0 (10/2017). Guidelines for evaluation of radio interface technologies for IMT 2020.

23. Kyösti P., Meinilä J., Hentilä L., Holma P., Käske M., Narandžić M., et al. WINNER II Channel Models for System Level Simulations. Final Report on Model Specification. Version 1.2. 2008. URL: http://signserv.signal.uu.se/Publications/WINNER/WIN2D112.pdf

24. Holma P., Meinilä J., Kyösti P., Hentilä L., Jämsä T., Suikkanen E., et al. CP5-026 WINNER+ D5.3 v1.0 WINNER+ Final Channel Models. 2010.

25. Chi Y., Liu L., Song G., Yuen C., Guan Y.L., Li Y. Practical MIMO-NOMA: Low Complexity & Capacity-Approaching Solution // arXiv preprint. 2018. DOI:10.48550/arXiv.1807.06846

26. de Sena A.S., Nardelli P.H.J., da Costa D.B., Lima F.R.M., Yang L., Popovski P., Ding Z., Papadias C.B. IRS-Assisted Massive MIMO-NOMA Networks with Polarization Diversity // arXiv preprint. 2021. DOI:10.48550/arXiv.2105.12952