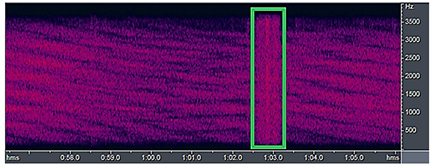
Распределение комплексной огибающей сигналов, принятых из канала в условиях «сложной» сигнально-помеховой обстановки

Аннотация. При статистическом анализе комплексных огибающих модулированных сигналов, принимаемых из канала связи, в качестве модели плотности распределения вероятностей общепринято полагают нормальную плотность распределения. Однако в канале с глубокими замираниями, а также при наличии помех, т. е. в случае «сложной» сигнально-помеховой обстановки, интерес могут представлять модели распределений, обладающие более тяжелыми хвостами. В качестве таковых в работе рассматриваются логистическое распределение и распределение гиперболического секанса. В работе приведены выражения для соответствующих двумерных плотностей распределения вероятностей.

Цель работы: показать, что при определенных условиях в реальном канале связи могут наблюдаться
модели распределения комплексной огибающей, отличные от нормального. Учет данного обстоятельства может позволить улучшить характеристики системы связи в задачах адаптации и оценки надежности решений демодулятора.

Методы исследования: для проверки принадлежности комплексной огибающей соответствующему
закону распределения применяется критерий Хи-квадрат. В статье предложена реализация критерия Хи-квадрат для случая двумерной плотности распределения.

В качестве результатов в работе представлен анализ статистической обработки сигналов, принятых из реального канала связи в различных условиях.

Новизна состоит в экспериментальном исследовании факта, что в реальных каналах в случае глубоких замираний и сложной сигнально-помеховой обстановки более предпочтительными могут оказаться логистическое распределение или распределение гиперболического секанса.

Практическая значимость заключается в том, что учет модели распределения позволяет получить более адекватную оценку среднего квадратичного отклонения шумовой составляющей и отношения сигнал / шум, что имеет существенное значение для функционирования адаптивных систем радиосвязи, а также в задаче оценки мягких решений демодуляции.

1. Levy B.C. Principles of Signal Detection and Parameter Estimation. New York: Springer, 2008. DOI:10.1007/978-0-387-76544-0

2. Barkat M. Signal Detection and Estimation. Boston: Artech, 2005.

3. Серкин Ф.Б., Важенин Н.А., Вейцель В.В. Сравнительный анализ алгоритмов оценки отношения сигнал-шум на основе квадратурных компонент принимаемого сигнала // Труды МАИ. 2015. № 83. C. 19. EDN:UNWXRT

4. Beaulieu N.C., Toms A.S., Pauluzzi D.R. Comparison of four SNR estimators for QPSK modulations // IEEE Communications Letters. 2000. Vol. 4. Iss. 2. PP. 43‒45. DOI:10.1109/4234.824751

5. Pauluzzi D.R., Beaulieu N. A comparison of SNR estimation techniques in the AWGN channel // Proceedings of the Pacific Rim Conference on Communications, Computers, and Signal Processing (Victoria, Canada, 17‒19 May 1995). IEEE, 1995. DOI:10.1109/PACRIM.1995.519404

6. Cavers J.K. Mobile Channel Characteristics. New York: Kluwer, 2002.

7. Тихонов В.И. Статистическая радиотехника. М.: Советское радио, 1966.

8. Simon M.K., Alouini M.S. Digital Communication over Fading Channels: A Unified Approach to Performance Analysis. New York: John Wiley & Sons, 2000.

9. Патюков В.Г., Патюков Е.В., Силантьев А.А. Оценка отношения сигнал/шум на основе фазовых флуктуаций сигнала // Журнал радиоэлектроники. 2013. № 4. С. 1. EDN:PZZBWL

10. Jammalamadaka S.R., Sengupta A. Topics in Circular Statistics. Singapore: World Scientific, 2001.

11. Mardia K.V., Jupp P.E. Directional Statistics. John Wiley & Sons, Inc, 2000.

12. Tong Y.L. The Multivariate Normal Distribution. New-York: Springer-Verlag, 1990.

13. Thomas C.M. Maximum Likelihood Estimation of Signal-to-Noise Ratio. Ph.D. Thesis. Los Angeles: University of Southern California, 1967.

14. Bellili F., Meftehi R., Affes S., Stephenne A. Maximum likelihood SNR estimation over time-varying flat-fading SIMO channels // Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP, Florence, Italy, 04-09 May 2014). IEEE, 2014. PP. 6523‒6527. DOI:10.1109/ICASSP.2014.6854861

15. Treviño J.C., Benammar M., Roque D. A Hybrid Envelope-IQ Moment-Based Non-Data-Aided SNR Estimator for QPSK // IEEE Communications Letters. 2024. Vol. 28. Iss. 6. PP. 1382‒386. DOI:10.1109/LCOMM.2024.3386188

16. Силантьев А.А., Шатров В.А., Патюков В.Г., Рябушкин С.А. Метод оценки отношения сигнал/шум на основе статистических характеристик выбросов случайных процессов применительно к командно-измерительной системе спутниковой связи // Исследования Наукограда. 2014. № 4(10). С. 4‒8. EDN:TBSMSV

17. Агеев Ф.И., Вознюк В.В., Куценко Е.В. Методика расчета вероятности ошибки оптимального посимвольного когерентного приема MPSK сигналов при наличии в канале радиосвязи узкополосной шумовой помехи // Труды МАИ. 2024. № 139. С. 15. EDN:QBDQJZ

18. Bakkali M., Stephenne A., Affes S. Iterative SNR Estimation for MPSK Modulation Over AWGN Channels // Proceedings of the Vehicular Technology Conference (Montreal, Canada, 25‒28 September 2006). IEEE, 2006. DOI:10.1109/VTCF.2006.350

19. Jiang L., Zheng G., Zhang B. A Noise Estimation Method Based on Envelope Pseudo-measurement System in Adaptive Kalman Filter // Proceedings of the 43rd Chinese Control Conference (CCC, Kunming, China, 28‒31 July 2024). IEEE, 2024. PP. 208‒213. DOI:10.23919/CCC63176.2024.10661809

20. Türkben Ö.Ü.A.K., Al-Akraa V. S.A. SNR Estimation in Communication Systems Using Cognitive Radio // Proceedings of the 5th International Conference on Engineering Technology and its Applications (IICETA, Al-Najaf, Iraq, 31 May ‒ 01 June 2022). IEEE, 2022. PP. 477‒481. DOI:10.1109/IICETA54559.2022.9888467

21. Лемешко Б.Ю., Лемешко С.Б., Постовалов С.Н., Чимитова Е.В. Статистический анализ данных, моделирование и исследование вероятностных закономерностей. Компьютерный подход. Новосибирск: Изд-во НГТУ, 2011. EDN:TZNHMX

22. Balakrishnan N. Handbook of the Logistic Distribution. Boca Raton: CRC Press, 1991. 624 p. DOI:10.1201/9781482277098

23. Giri N.C. Multivariate Statistical Analysis. Boca Raton: Marcel Dekker, 2003. 550 p. DOI:10.1201/9781482276374

24. Fischer M.J. Generalized Hyperbolic Secant Distributions. New York: Springer, 2014. DOI:10.1007/978-3-642-45138-6

25. Капля Е.В. Обобщение закона гиперболического секанса и логистического закона распределения в единый закон распределения с варьируемым коэффициентом эксцесса // Дальневосточный математический журнал. 2020. Т. 20. № 1. С. 74‒81. DOI:10.47910/FEMJ202008. EDN:NLRAHN

26. Ding P. Three Occurrences of the Hyperbolic-Secant Distribution // The American Statistician. 2014. Vol. 68. Iss. 1. PP. 32‒35. DOI:10.1080/00031305.2013.867902

27. Forbes C., Evans M., Hastings N., Peacock B. Statistical Distributions. New Jersey: John Wiley & Sons, 2011. 230 p.

28. Greenwood P.E., Nikulin M.S. A Guide to Chi-Squared testing. New York: John Wiley & Sons, 1996. 304 p.

29. Никулин М.С. О критерии согласия Хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее применение. 1973. Т. 18. № 3. С. 583‒591.

30. Watson G.S. On Chi-Square Goodness-of-Fit Tests for Continuous Distributions // Journal of the Royal Statistical Society: Series B. 1958. Vol. 20. Iss. 1. PP. 44‒61. DOI:10.1111/j.2517-6161.1958.tb00274.x

31. Мирвалиев М. Критерии согласия Хи-квадрат для одного семейства многомерных дискретных распределений // Теория вероятностей и ее применение. 1989. Т. 34. № 4. С. 794‒799.

32. Воинов В.Г., Никулин М.С. Критерий согласия Хи-квадрат для одномерных и многомерных дискретных распределений // Записки научных семинаров ЛОМИ. 1990. Т. 184. С. 62‒79.

33. Лемешко Б.Ю., Чимитова Е.В. О выборе числа интервалов в критериях согласия типа С2 // Заводская лаборатория. Диагностика материалов. 2003. Т. 69. № 1. С. 61‒67. EDN:SDJQIF

34. Hasan A.A., Marsland I.D. Low Complexity LLR Metrics for Polar Coded QAM // Proceedings of the 30th Canadian Conference on Electrical and Computer Engineering (CCECE, Windsor, Canada, 30 April ‒ 03 May 2017). IEEE, 2017. DOI:10.1109/CCECE.2017.7946778