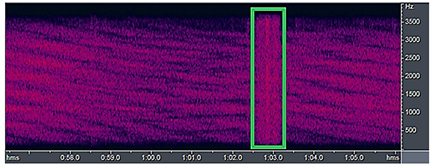
Distribution of the Complex Envelope for Signals Received from a Channel with a "Complex" Signal-Noise Environment
https://doi.org/10.31854/1813-324X-2025-11-3-47-58
EDN: OJBGGT
Abstract
Relevance. In statistical analysis of complex envelopes of modulated signals received from a communication channel, the normal distribution density is generally assumed to be the probability density model. However, in a channel with deep fading and in the presence of interference, i.e. in the case of a "complex" signal-interference environment in the channel, distribution models with heavier tails may be of interest. The logistic distribution and the hyperbolic secant distribution are considered as such in the work. Expressions for the corresponding two-dimensional probability distribution densities are presented.
The aim of the work is to show that, under certain conditions, models of the distribution of the complex envelope that other than normal one can be observed in a real communication channel. Taking this into account may allow to improve the characteristics of the communication system in the tasks of adaptation and evaluation of the reliability of demodulator solutions.
Research methods: To check whether the complex envelope belongs to the corresponding distribution law, the Chi-square criterion is used. The implementation of the Chi-square criterion for the case of a two-dimensional distribution density is proposed in article.
As results, the paper presents the analysis of statistical processing of signals received from a real communication channel under various conditions.
The novelty lies in the experimental study of the fact that in real channels, in the case of deep fading and complex signal-interference conditions, the logistic distribution or the hyperbolic secant distribution may be more preferable.
The practical significance lies in the fact that taking into account the distribution model makes it possible to obtain a more adequate estimate of the mean square deviation of the noise component and the signal-to-noise ratio, which is essential for the functioning of adaptive radio communication systems, as well as in the task of evaluating soft demodulation solutions.
About the Author
M. L. MaslakovRussian Federation
References
1. Levy B.C. Principles of Signal Detection and Parameter Estimation. New York: Springer; 2008. DOI:10.1007/978-0-387-76544-0
2. Barkat M. Signal Detection and Estimation. Boston: Artech; 2005.
3. Serkin F.B., Vazhenin N.A., Veytsel V.V. Analysis of signal-to-noise ratio estimation algorithms based on inphase and quadrature components of the received signal. Trudy MAI. 2015;83:19. (in Russ.) EDN:UNWXRT
4. Beaulieu N.C., Toms A.S., Pauluzzi D.R. Comparison of four SNR estimators for QPSK modulations. IEEE Communications Letters. 2000;4(2):43‒45. DOI:10.1109/4234.824751
5. Pauluzzi D.R., Beaulieu N. A comparison of SNR estimation techniques in the AWGN channel. Proceedings of the Pacific Rim Conference on Communications, Computers, and Signal Processing, 17‒19 May 1995, Victoria, Canada. IEEE; 1995. DOI:10.1109/PACRIM.1995.519404
6. Cavers J.K. Mobile Channel Characteristics. New York: Kluwer; 2002.
7. Tikhonov V.I. Statisticheskaya radiotekhnika. Moscow: Sovetskoe radio Publ.; 1966. (in Russ.)
8. Simon M.K., Alouini M.S. Digital Communication over Fading Channels: A Unified Approach to Performance Analysis. New York: John Wiley & Sons; 2000.
9. Patyukov V.G., Patyukov E.V., Silantiev A.A. Measurement of the attitude a signal/noise on the basis of phase fluctuations of a signal. Journal of Radio Electronics. 2013;4:1. (in Russ.) EDN:PZZBWL
10. Jammalamadaka S.R., Sengupta A. Topics in Circular Statistics. Singapore: World Scientific; 2001.
11. Mardia K.V., Jupp P.E. Directional Statistics. John Wiley & Sons, Inc; 2000.
12. Tong Y.L. The Multivariate Normal Distribution. New-York: Springer-Verlag; 1990.
13. Thomas C.M. Maximum Likelihood Estimation of Signal-to-Noise Ratio. Ph.D. Thesis. Los Angeles: University of Southern California; 1967.
14. Bellili F., Meftehi R., Affes S., Stephenne A. Maximum likelihood SNR estimation over time-varying flat-fading SIMO channels. Proceedings of the International Conference on Acoustics, Speech and Signal Processing, ICASSP, 04‒09 May 2014, Florence, Italy. IEEE; 2014. p.6523‒6527. DOI:10.1109/ICASSP.2014.6854861
15. Treviño J.C., Benammar M., Roque D. A Hybrid Envelope-IQ Moment-Based Non-Data-Aided SNR Estimator for QPSK. IEEE Communications Letters. 2024;28(6):1382‒1386. DOI:10.1109/LCOMM.2024.3386188
16. Silantyev A.A., Shatrov V.A., Patyukov V.G., Ryabushkin S.A. Method of estimation of the signal/noise ratio, based on the statistical characteristics of the emission of stochastic processes, as applied to the telemetry, commandand ranging system of satellite communication. Issledovaniya Naukograda. 2014;4(10):4‒8. (in Russ.) EDN:TBSMSV
17. Ageev F.I., Voznuk V.V., Kutsenko E.V. A method for calculating the probability of a bit error of optimal character-by-character coherent reception of multiple phase-manipulated signals in the presence of narrowband noise interference in the radio communication channe. Trudy MAI. 2024;139:15. (in Russ.) EDN:QBDQJZ
18. Bakkali M., Stephenne A., Affes S. Iterative SNR Estimation for MPSK Modulation Over AWGN Channels. Proceedings of the Vehicular Technology Conference, 25‒28 September 2006, Montreal, Canada. IEEE; 2006. DOI:10.1109/VTCF.2006.350
19. Jiang L., Zheng G., Zhang B. A Noise Estimation Method Based on Envelope Pseudo-measurement System in Adaptive Kalman Filter. Proceedings of the 43rd Chinese Control Conference, CCC, 28‒31 July 2024, Kunming, China. IEEE; 2024. p.208‒213. DOI:10.23919/CCC63176.2024.10661809
20. Türkben Ö.Ü.A.K., Al-Akraa V. S.A. SNR Estimation in Communication Systems Using Cognitive Radio. Proceedings of the 5th International Conference on Engineering Technology and its Applications, IICETA, 31 May ‒ 01 June 2022, Al-Najaf, Iraq. IEEE; 2022. p.477‒481. DOI:10.1109/IICETA54559.2022.9888467
21. Lemeshko B.Yu., Lemeshko S.B., Postovalov S.N., Chimitova E.V. Statistical data Analysis, Simulation and Study of Probability Regularities. Computer Approach. Novosibirsk: NSTU Publ.; 2011. (in Russ.) EDN:TZNHMX
22. Balakrishnan N. Handbook of the Logistic Distribution. Boca Raton: CRC Press; 1991. 624 p. DOI:10.1201/9781482277098
23. Giri N.C. Multivariate Statistical Analysis. Boca Raton: Marcel Dekker; 2003. 550 p. DOI:10.1201/9781482276374
24. Fischer M.J. Generalized Hyperbolic Secant Distributions. New York: Springer; 2014. DOI:10.1007/978-3-642-45138-6
25. Kaplya E.V. The generalization of the hyperbolic secant distribution and the logistic distribution in the single dostribution with variable kurtosis. Far Eastern Mathematical Journal. 2020;20(1):74–81. (in Russ.) DOI:10.47910/FEMJ202008. EDN:NLRAHN
26. Ding P. Three Occurrences of the Hyperbolic-Secant Distribution. The American Statistician. 2014;68(1):32‒35. DOI:10.1080/00031305.2013.867902
27. Forbes C., Evans M., Hastings N., Peacock B. Statistical Distributions. New Jersey: John Wiley & Sons; 2011. 230 p.
28. Greenwood P.E., Nikulin M.S. A Guide to Chi-Squared testing. New York: John Wiley & Sons; 1996. 304 p.
29. Nikulin M.S. Chi-Square Test for Continuous Distributions with Shift and Scale Parameters Theory of Probability and its Applications. 1974;18(3):559‒568. DOI:10.1137/1118069
30. Watson G.S. On Chi-square goodness-of-fit tests for continuous distributions. Journal of the Royal Statistical Society: Series B. 1958;20(1):44‒61. DOI:10.1111/j.2517-6161.1958.tb00274.x
31. Mirvaliev M. Chi-Square Goodness-of-Fit Tests for a Family of Multidimensional Discrete Distributions. Theory of Probability and its Applications. 1989;34(4):728‒732. DOI:10.1137/1134094
32. Voinov V.G., Nikulin M.S. Chi-square goodness-of-fit test for one- and multidimensional discrete distributions. Journal of Mathematical Sciences. 1994;68:438‒450. DOI:10.1007/BF01254268
33. Lemeshko B.Yu., Chimitova E.V. On the choice of the number of intervals in Type C2 Good-Affirmation Criteria. Zavodskaya laboratoriya. Diagnostika materialov. 2003:69(1):61‒67. (in Russ.) EDN:SDJQIF
34. Hasan A.A., Marsland I.D. Low Complexity LLR Metrics for Polar Coded QAM. Proceedings of the 30th Canadian Conference on Electrical and Computer Engineering, CCECE, 30 April ‒ 03 May 2017, Windsor, Canada. IEEE; 2017. DOI:10.1109/ CCECE.2017.7946778
35.
Review
For citations:
Maslakov M.L. Distribution of the Complex Envelope for Signals Received from a Channel with a "Complex" Signal-Noise Environment. Proceedings of Telecommunication Universities. 2025;11(3):47-58. (In Russ.) https://doi.org/10.31854/1813-324X-2025-11-3-47-58. EDN: OJBGGT


































