Implementation of an ECC Digital Signature Technique in Constrained Environments

Relevance. Ensuring secure cryptographic operations in resource-constrained environments presents challenges due to limited computational power and memory. With the rapid growth of Unmanned Vehicle Systems, the need for efficient and secure cryptographic solutions is increasing. Optimizing cryptographic algorithms for such systems becomes especially relevant given their limited computational resources and high security demands.

The purpose of this study is to optimize Elliptic Curve Cryptography (ECC) digital signature operations for resource-limited systems, particularly in unmanned vehicle systems. The research aims to enhance computational efficiency and reduce memory usage, making ECC-based security mechanisms more feasible for embedded applications.

The novelty of this study lies in its integration of multiple optimization techniques. It improves scalar point multiplication by leveraging cyclic group properties, additive inverses, and an enhanced windowed multiplication method. Additionally, it introduces a deterministic nonce generation approach inspired by EdDSA to further refine digital signature efficiency. These innovations collectively contribute to a more efficient cryptographic process suitable for constrained environments.

The theoretical significance lies in the development of a new mathematical apparatus that makes it possible to optimize electronic signature operations.

The practical significance of this study is its applicability in low-power embedded systems, where computational and memory resources are highly limited. By optimizing ECC operations, this research enhances the security and performance of cryptographic implementations in unmanned vehicle systems and similar embedded applications, ensuring secure communications without exceeding hardware constraints.

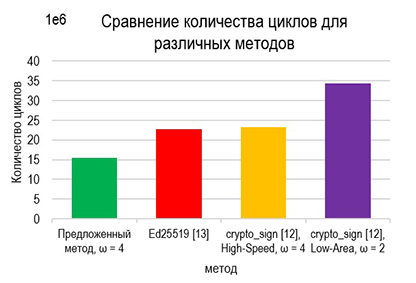
The proposed method was implemented on the Arduino Atmega 2560 R3, achieves up to a 54,1 % results are showing reduction in cycle count and a 72,6 % decrease in SRAM usage for key generation, alongside significant performance improvements in signing and verification processes. Experimental results confirm its effectiveness in optimizing ECC operations for constrained devices of unmanned vehicle systems.

1. Johnson D., Menezes A., Vanstone S. The Elliptic Curve Digital Signature Algorithm (ECDSA). International Journal of Information Security. 2001;1:36‒63. DOI:10.1007/s102070100002

2. Josefsson S., Liusvaara I. Edwards-Curve Digital Signature Algorithm (EdDSA). 2017. DOI:10.17487/RFC8032

3. Sabbry N.H., Levina A.B. An Optimized Point Multiplication Strategy in Elliptic Curve Cryptography for Resource-Constrained Devices. Mathematics. 2024;12(6):881. DOI:10.3390/math12060881. EDN:JZKADF

4. Hisil H., Wong K.K., Carter G., Dawson E. Twisted Edwards Curves Revisited. Proceedings of the 14th International Conference on the Theory and Application of Cryptology and Information Security, ASIACRYPT 2008, 7‒11 December 2008, Mel-bourne, Australia. Lecture Notes in Computer Science, vol.5350. Berlin, Heidelberg: Springer; 2008. p.326‒343. DOI:10.1007/978-3-540-89255-7_20

5. Sabbry N.H., Levina A. Nonce generation techniques in Schnorr multi-signatures: Exploring EdDSA-inspired approaches. AIMS Mathematics. 2024;9(8):20304‒20325. DOI:10.3934/math.2024988. EDN:YSJYIC

6. Paar C., Pelzl J. Understanding Cryptography: A Textbook for Students and Practitioners. Berlin, Heidelberg: Springer; 2010. DOI:10.1007/978-3-642-04101-3

7. Hankerson D., Menezes A. Elliptic Curve Cryptography. In: Jajodia S., Samarati P., Yung M. (eds.) Encyclopedia of Cryptography, Security and Privacy. Berlin, Heidelberg: Springer; 2021. p.1‒2. DOI:10.1007/978-3-642-27739-9_245-2

8. Izu T., Möller B., Takagi T. Improved Elliptic Curve Multiplication Methods Resistant Against Side Channel Attacks. Proceedings of the Third International Conference on Cryptology in India, INDOCRYPT 2002, 16–18 December 2002, Hyderabad, India. Lecture Notes in Computer Science, vol.2551. Berlin Heidelberg: Springer; 2002. p.296‒313. DOI:10.1007/3-540-36231-2_24

9. Shenets N.N., Petushkov A.S. New Regular Sliding Window Algorithms for Elliptic Curve Scalar Point Multiplication. Automatic Control and Computer Sciences. 2021;55:1029‒1038. DOI:10.3103/S0146411621080289. EDN:FWONTD

10. Cheon J.H., Hong J., Kim M. Speeding Up the Pollard Rho Method on Prime Fields. Proceedings of the 14th International Conference on the Theory and Application of Cryptology and Information Security, ASIACRYPT 2008, 7‒11 December 2008, Melbourne, Australia. Berlin, Heidelberg: Springer; 2008. p.471‒488. DOI:10.1007/978-3-540-89255-7_29

11. Alyas H.H., Abdullah A.A. Enhancement the ChaCha20 Encryption Algorithm Based on Chaotic Maps. In: Kumar R., Mishra B.K., Pattnaik P.K. Next Generation of Internet of Things: Proceedings of ICNGIoT 2021. Lecture Notes in Networks and Systems, vol.201. Singapore: Springer; 2021. p.91‒107. DOI:10.1007/978-981-16-0666-3_10. EDN:ZPPOQO

12. Hutter M., Schwabe P. NaCl on 8-Bit AVR Microcontrollers. Proceedings of the 6th International Conference on Cryptology in Africa «Progress in Cryptology», AFRICACRYPT 2013, 22‒24 June 2013, Cairo, Egypt. Lecture Notes in Computer Science, vol.7918. Berlin, Heidelberg: Springer; 2013. p.156‒172. DOI:10.1007/978-3-642-38553-7_9

13. Nouma S.E., Yavuz A.A. Lightweight and Resilient Signatures for Cloud-Assisted Embedded IoT Systems. arXiv preprint arXiv:2409.13937. 2024. DOI:10.48550/arXiv.2409.13937