Модель представления решающих функций для метрических методов распознавания образов

В настоящее время ключевую роль поддержки принятия решений в различных отраслях играет интеллектуальный анализ данных. Его важной составной частью является машинное обучение, актуальная задача которого на практике ‒ осуществление классификации объектов в режиме реального времени. Она может быть достигнута за счет распараллеливания алгоритмов обработки данных как по входным данным, так и по данным решающих функций. Для повышения эффективности распараллеливания методов машинного обучения разработана унифицированная модель представления решающих функций. Целью настоящей статьи является представление унифицированной модели решающих функций для алгоритмов машинного обучения и функций, обеспечивающих ее распараллеливание как по входным данным, так и по данным решающих функций.

Сущность представленного подхода заключается в том, что на основе анализа особенностей работы метрических методов машинного обучения выявлены независимые данные для обработки, представленные в виде разных категорий анализируемого свойства, разработана модель представления решающих функций, описывающая выявленные характерные черты объектов входных данных и данных решающих функций в виде соответствующих наборов унифицированных элементов и включающая в себя функции, обеспечивающие их параллельную обработку на основе группового распараллеливания объектов. Предложенный подход базируется на использовании методов анализа алгоритмов и вычислительной сложности, математической статистики и методологии проектирования параллельных алгоритмов.

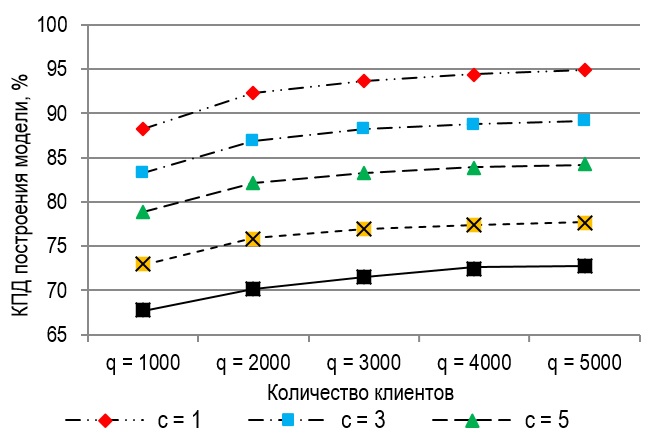
Эксперименты показали, что распараллеливание предложенной модели решающих функций на примере метода потенциальных функций позволяет повысить эффективность классификации как для одного объекта за счет возможности использования дополнительных вычислительных ресурсов, так и для группы объектов при наличии ограничений объема памяти компьютеров или горизонта планирования.

Научная новизна предложенного подхода заключается в том, что модель отличается от существующих единым способом формализации объектов и их свойств в виде унифицированных элементов для обучающих и классификационных данных и имеет структуру и функции, ориентированные на ее параллельную обработку методами распознавания образов на основе решающих функций в рамках группового распараллеливания объектов.

Теоретическая значимость: модель имеет унифицированный характер и может использоваться при распараллеливании других методов распознавания образов, которые могут быть описаны сходными параметрами, архитектурой и классификационными признаками.

Практическая значимость предложенного подхода заключается в том, что модель позволяет осуществить декомпозицию задачи классификации образов на отдельные подзадачи поиска закономерностей между входными данными и данными решающих функций.

1. Балашова И.В., Терещенко Т.А. Системы поддержки принятия решений // The Scientific Heritage. 2021. № 79-4(79). С. 3‒7. DOI:10.24412/9215-0365-2021-79-4-3-7. EDN:VBGSEN

2. Конев К.А. Машинное обучение для поддержки принятия решений в сфере качества на промышленном предприятии // Экономика. Информатика. 2023. T. 50. № 3. С. 689‒703. DOI:10.52575/2687-0932-2023-50-3-689-703. EDN:EOVNCU

3. Макшанов А.В., Журавлев А.Е. Технологии интеллектуального анализа данных: учебное пособие. СПб.: Лань, 2019. 212 с.

4. Замятин А.В. Интеллектуальный анализ данных: учебное пособие. Томск: Национальный исследовательский Томский государственный университет, 2020. 196 с. EDN:RODEPA

5. Платонов А.В. Машинное обучение: учебное пособие для вузов. М.: Издательство Юрайт, 2025. 89 с.

6. Лимановская О.В., Алферьева Т.И. Основы машинного обучения: учебное пособие. Екатеринбург: Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, 2020. 88 с. EDN:YLJQGT

7. Фомин В.В., Миклуш В.А. Интеллектуальные информационные системы: учебное пособие. СПб.: Российский государственный гидрометеорологический университет, 2013. 150 с. EDN:UPSHTP

8. Кочубей Р.И., Бычковский М.М., Зайкин Н.Н., Фатьянова Е.В., Свидло А.В., Чуприков О.В. Обоснование метода распознавания для решения задачи контроля содержимого данных о состоянии техники связи специального назначения // Известия Тульского государственного университета. Технические науки. 2023. № 12. С. 533‒535. DOI:10.24412/2071-6168-2023-12-533-534. EDN:HVOKOQ

9. Дюк В.А., Малыгин И.Г., Прицкер В.И. Распознавание транспортных средств по силуэтам – трехкаскадный метод машинного обучения в системах технического зрения // Морские интеллектуальные технологии. 2022. № 2-1(56). С. 162‒167. DOI:10.37220/MIT.2022.56.2.022. EDN:WQMNAG

10. Зайнидинов Х.Н., Каршиев З.А. Особенности параллельного выполнения алгоритмов интеллектуального анализа данных // Автоматика и программная инженерия. 2020. № 1(31). С. 83‒91. EDN:YRWQDE

11. Холод И.И. Модели и методы построения параллельных алгоритмов анализа распределенных данных. Дис. … докт. техн. наук. СПб.: Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им. В.И. Ульянова (Ленина), 2018. 351 с. EDN:HKSFMU

12. Kholod I.I., Shorov A.V. Unification of mining model for parallel processing // Proceedings of the Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus, St. Petersburg and Moscow, Russian Federation, 01‒03 February 2017). IEEE, 2017. PP. 450‒455. DOI:10.1109/EIConRus.2017.7910588. EDN:XMZHNX

13. Холод И.И. Метод определения возможностей параллельного выполнения функций алгоритмов анализа данных // Программные продукты и системы. 2018. № 2. С. 268‒274. DOI:10.15827/0236-235X.122.268-274. EDN:UYSUBG

14. Bishop C. Pattern Recognition and Machine Learning. Berlin: Springer, 2006. 738 p.

15. Customer Churn DataSet // Kaggle. URL: https://www.kaggle.com/datasets/muhammadshahidazeem/customer-churn-dataset (Accessed 10.04.2025)