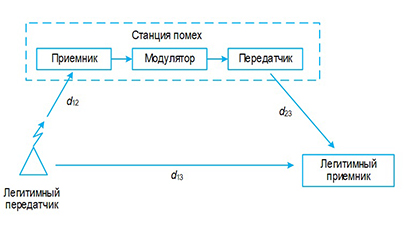
Wireless System Using Spread Spectrum Signals under the Conditions of Possible Jamming by Retransmitted Interference

Presently, it is very important to design wireless systems that are resistant to jamming by adversary. It is well known technology to execute so called spread spectrum signals in order to prevent such attacks, especially under the conditions when enemy is superior i1n power against legitimate users. Moreover, adversary is able to estimate legitime signal parameter (type of modulation, duration of intervals ctr) However, such approach be vulnerable in the case of the use by adversary so called retransmitted interferences.   

The purpose of this article is to increase the efficiency of spread spectrum signals transmission under the action of retransmitted interference, the power of which exceeds the power of the legitimate signals.

The essence of the proposed solution is to use spread spectrum phase-frequency modulated signals for information transmission, generated using independent unpredictable pseudorandom sequences that are different at the transmitted and non-transmitted frequencies. Instant phases are randomized independently for bit intervals at the transmitting side. Theoretically, using appropriated mathematical technique, the formula is derived for calculating of the bit error probability for the proposed system with different choice of its parameters. It is proved that for correctly selected parameters, the probabilities of bit errors are approaching to such values that occurs qcceptable to use next error correcting codes, which will ensure reliable delivery of important information. 

The scientific novelty of our method consists in the use an unpredictable pseudorandom sequence at a frequency that is not currently being transmitted, in a randomized phase shift at each bit interval when forming a broadband signal, as well as in optimizing the parameters for the proposed radio communication system, that improved significantly further use of error-correcting code.

The theoretical significance consists in the correct proof of the formula for the bit error probabilities and further estimation the conditions for application of error correction codes.

The practical significance lies in design of interference proof wireless communication system that after some further elaboration of synchronization system and error correction codes, can be applied in practice under very hard interference environment.

1. Proakis J. Digital Communications. N.Y.: McGraw-Hill; 1995.

2. Dixon R.C. Spread Spectrum Systems. John Willy and Sons; 1979.

3. Sklar B. Digital Communications. Fundamentals and Applications. Prentice Hall; 2001.

4. Goldsmith A. Wireless Communications. Cambridge University Press; 2005.

5. Borisov V.I., Zinchuk V.M, Limarev A.E., Muhin N.P., Shestopalov V.I. ECM-Resistance of Frequency-Hopping of Spread ‒ Spectrum Communications Systems. Moscow: Radio and Communications Publ.; 2003. 384 p. (in Russ.) EDN:QMMHCF

6. Korjik V., Bikkenin R. Performance analysis of the enhanced PN spread spectrum system in the presence of jamming by modulated retransmitted signal. Proceedings of the 5th International Symposium on Spread Spectrum Techniques and Applications, 04‒04 September 1998, Sun City, South Africa. IEEE; 1998. p.809‒811. DOI:10.1109/ISSSTA.1998.722490

7. Fink L.M. Theory of Transmission of Discrete Messages. Moscow: Soviet Radio Publ.; 1970. 728 p. (in Russ.)

8. Agafonov A.A., Lozhkin K.Yu., Poddubny V.N. Methodology and Results of Synthesis and Estimation of the Efficiency of Malicious Interferences for Discrete Signal Receivers. Journal of Radio Electronics. 2003;48(8):956‒962. (in Russ.) EDN:OOQISJ

9. Abramowitz M. Stegun I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. National Bureau of Standards Applied Mathematics Series. 55. Issued June 1964.

10. Shannon C.E. A mathematical theory of communication. Bell System Technical Journal. 1948;27:379–423 and 623–656.

11. MacKay D.J.C., Neal R.M. Near Shannon Limit Performance of Low-Density Parity Check Codes. Electronics Letters. 1996;32(18). DOI:10.1049/el:19961141

12. MacKay D.J.C. Information Theory, Inference and Learning Algorithms. Cambridge University Press; 2003. 640 p.

13. Berrou C., Glavieux A., Thitmajshima P. Near optimum error correcting coding and decoding: Turbo-codes. IEEE Transactions on Commutations. 1996;44(10):1261‒1271. DOI:10.1109/26.539767

14. Zhuravlev V.I. Search and Synchronization in Spread Spectrum Systems. Moscow: Radio and Communications Publ.; 1986. 240 p. (in Russ.) EDN:WIYMEJ

15. Borisov V.I., Zinchuk V.M., Limarev A.E., Mukhin N.P., Nakhmanson G.S. Noise Immunity of radio communication systems with Spread Spectrum Signal by Carrier Pseudorandom Sequence Modulation. Moscow: Radio and Communications Publ.; 2003. 640 p. (in Russ.)

16.