Advance in Applied Cryptography Theory: Survey and New Results. Part 1. Key Cryptography

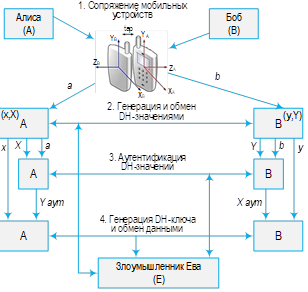
In the current paper, consisting from two parts, are presented both results already published before (but hard for access) and new once. Actuality of this work is firstly in a fact that recently has been obtained a number of new results in area of applied cryptography that are needed both in a clarification and be put into practice. This is namely the main goal of the current paper. The setting problem in the first paper part concerns to a complexity of symmetric cipher breaking while in the second part of the paper is discussed, so called, keyless cryptography, namely: wiretap channel concept, execution of communication channels which allow to provide information security without of key exchange procedure  between legal correspondences. In the part widely used methods of applied mathematics, namely: algebra, number, probability and information theories. Computer simulation also used there. A novelty of the first part of work consists in the following: first of all it is clarified the sense of a key lifetime limitation for different symmetric cipher modes, secondly, it is explained an approach of cipher breaking by the use of quantum computers, finely, the key authentication for the Diffie ‒ Hellman protocol based on the mobile device pairing technology is investigated in detail. In the second part of the current paper has been presented a vulnerability of Dean ‒ Goldsmith cryptosystem under some extension of attacks. The main results of this paper are: estimation of the key lifetime of single key for symmetric cipher in CBC mode, clarifying of Grover’s algorithm breaking of symmetric ciphers by brute force attack, development of a method for authentication of Diffie ‒ Hellman values based on pre-distributed sequences, selection of ciphers which allow to execute with Shamir’s protocol without any key sharing in advance, breaking of Dean ‒ Goldsmith protocol under some conclusions, proof the fact regarding of a possible breakability of the key sharing protocol over noiseless communication channels. Practical application of paper results consists in the fact of stimulation the correct choice of ciphers and their parameters in order to provide their resistance to different attacks and more attention to algorithms of keyless cryptography.

1. GOST 28147-89 Information processing systems. Cryptographic protection. Algorithm of cryptographic transformation. (in Russ.)

2. GOST Р 34.12-2015 Information technology. Cryptographic data security. Block ciphers. Moscow: Standartinform Publ.; 2015. (in Russ.)

3. GOST Р 34.10-2012 Information technology. Cryptographic data security. Generation and verification processes of elec-tronic digital signature. Moscow: Standartinform Publ.; 2012. (in Russ.)

4. GOST Р 34.11-2012 Information technology. Cryptographic data security. Hash-function. Moscow: Standartinform Publ.; 2012. (in Russ.)

5. Babash A.V., Shankin G.P. Cryptography. Moscow: Solon-R Publ.; 2002. 511 p. (in Russ.)

6. Korjik V.I., Mukherjii A., Eremeev M.A., Moldovyan N.A. Fault-based analysis of flexible ciphers. Computer Science Journal of Moldova. 2002;10(2):223‒236.

7. Korzhik V., Yakovlev V., Kovajkin Yu., Morales-Luna G. Secret Key Agreement Over Multipath Channels Exploiting a Variable-Directional Antenna. International Journal of Advanced Computer Science and Applications. 2012;3(1):172‒178. DOI:10.14569/IJACSA.2012.030127

8. Korzhik V.I., Yakovlev V.A. Fundamentals of Cryptography. St. Petersburg: Intermedia Publ.; 2016. 312 p. (in Russ.) EDN:WEQWMN

9. Korzhik V.I., Kushnir D.V. Fundamentals of information protection in computer systems. Methodical instructions for laboratory works. Part 1. St. Petersburg: The Bonch-Bruevich Saint Petersburg State University of Telecommunications Publ.; 1999. 17 p. (in Russ.)

10. Alpern B., Schneider F.B. Key exchange using ‘keyless cryptography‘. Information Processing Letters. 1983;16(2):79‒81. DOI:10.1016/0020-0190(83)90029-7

11. Korzhik V., Starostin V., Yakovlev V., Kabardov M., Krasov A. and Adadurov S. Advance in Keyless Cryptography. In: Ramakrishnan S., ed. Lightweight Cryptographic Techniques and Cybersecurity Approaches. IntechOpen; 2022. DOI:10.5772/intechopen.104429

12. Shannon C.E. Communication theory of secrecy systems. Bell System Technical Journal. 1949;28(4):656–715. DOI:10.1002/j.1538-7305.1949.tb00928.x

13. Vernam G.S. Secret signaling System. Patent US, no. 1310719A, 22.07.1919.

14. Lavrikov L.V., Shishkin V.A. How much data may be safely processed on one key in different modes? Mathematical Aspects of Cryptography. 2019;10(2):125–134 (in Russ.) DOI:10.4213/mvk290

15. Williams C.P. Explorations in Quantum Computing. Texts in Computer Science. 2011. DOI:10.1007/978-1-84628-887-6.

16. Grover algorithm. (in Russ.) URL: http://www.youtube.com/watch?v=cQDpimNzKMo [Accessed 10.05.2024]

17. Denisenko D.V., Nikitenkova M.V. Application of Grover’s Quantum Algorithm for SDES Key Searching. Journal of Experimental and Theoretical Physics. 2019;128(1):25‒44. (in Russ.) DOI:10.1134/S1063776118120142. EDN:GGWKYZ

18. Nielsen M.A., Chuang I.L. Quantum Computation and Quantum Information. Cambridge Universities Press; 2001.

19. Kaye F., Laflamme R., Mosca M. Introduction to quantum computing. Moccow – Izhevsk: Regulyarnaya i haoticheskaya dinamika Publ.; Institut komp'yuternyh Issledovanij Publ.; 2012. 360 p. (in Russ.)

20. Nielsen M.A., Chuang I.L. Quantum computation and Quantum Information. Contemporary Physics. 2011;52(6):604‒605. DOI:10.1080/00107514.2011.587535

21. Grover L.K. A fast quantum mechanical algorithm for database search. Proceedings of the twenty-eighth annual ACM symposium on Theory of Computing, STOC’96, 22‒24 May 1996, Philadelphia, USA. New York: ACM; 1996. DOI:10.1145/237814.237866

22. Zapryagaev A. Quantum computers. (in Russ.) URL: http//www.youtube.com/watch [Accessed 10.05.2024]

23. Grassl M., Langenberg B., Roetteler M., Steinwandt R. Applying Grover's algorithm to AES: quantum resource estimates. arXiv:1512.04965v1 [quantum-ph]. 2015. DOI:10.48550/arXiv.1512.04965

24. Google Research. A Preview of Bristlecone, Google’s New Quantum Processor. 2018. URL: https://research.google/blog/a-preview-of-bristlecone-googles-new-quantum-processor [Accessed 10.05.2024]

25. 3Dnews. IBM unveiled its most powerful quantum processor, Heron, and the first modular quantum computer. 2023. URL: https://3dnews.ru/1096936/ibm-predstavila-133kubitniy-kvantoviy-protsessor-heron-i-perviy-modulniy-kvantoviy-kompyuter [Accessed 10.05.2024]

26. Dyakonov M.I. Is Fault-Tolerant Quantum Computation Really Possible? In: Future Trends in Microelectronics. arXiv:quant-ph/0610117v1. 2006. DOI:10.48550/arXiv.quant-ph/0610117

27. Shor P.W., Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Journal on Computing. 1997;26(5):1484‒1509. DOI:10.1137/S0097539795293172

28. Goldovsky I. Post-quantum cryptography. Are we preparing today? PLUS. 2022;2(288). (in Russ.) URL: https://plusworld.ru/journal/2022/plus-2-2022/postkvantovaya-kriptografiya-gotovimsya-segodnya [Accessed 10.05.2024]

29. Diffe M., Hellman M. New directions in cryptography. IEEE Transactions on Information Theory. 1976;22(6):644‒654. DOI:10.1109/TIT.1976.1055638

30. Jin R., Shi L., Zeng K., Pande A., Mohapatra P. MagPairing: Pairing Smartphones in Close Proximity Using Magnetometer. IEEE Transactions on Information Forensics and Security. 2016;1(6):1304–1319. DOI:10.1109/TIFS.2015.2505626

31. Yakovlev V.A. Authentication of Keys Distriburted by the Diffie ‒ Hellman Method for Mobile Devices Based on Authentication Codes and Magnetometric Data. SPIIRAS Proceedings. 2019;18(3):705‒740. (in Russ.) DOI:10.15622/sp.2019.18.3.705-740. EDN:PRNILE

32. Yakovlev V., Korzhik V., Adadurov S. Authentication of Diffie-Hellman Protocol for Mobile Units Executing a Secure Device Pairing Procedure in Advance. Proceedings of the 29th Conference of Open Innovations Association, FRUCT, 12‒14 May 2021, Tampere, Finland. 2021. p.385‒392. EDN:DWHDGP

33. Yakovlev V. Method for Authentication of Diffie ‒ Hellman Values Based on Pre-Distributed Random Sequences and Wegman ‒ Carter One-Time Pad Algorithm. Proceedings of Telecommunication Universities. 2021;7(3):79‒90. (in Russ.) DOI:10.31854/1813-324X-2021-7-3-79-90. EDN:TBVSMD

34. Nielsen M., Chang I. Quantum computing and quantum information. Moscow: Mir Publ.; 2006. 824 p. (in Russ.)

35. Castelvecchi D. China's quantum satellite clears major hurdle on way to ultrasecure communications. Nature. 2017. DOI:10.1038/nature.2017.22142

36. Nield D. Quantum Teleportation Was Just Achieved With 90% Accuracy Over a 44km Distance. ScienceAlert. 2020. https://www.sciencealert.com/scientists-achieve-sustained-high-fidelity-quantum-teleportation-over-44-km [Accessed 10.05.2024]

37. Korpusov V., Olkhovoy O., Yakovlev V. The Research of the Random Number Generator Based on the Magnetometer. Proceedings of the VIIth International Conference on Infotelecommunications in Science and Education, 28 February ‒ 1 Murch 2018, St. Petersburg, Russia. St. Petersburg: The Bonch-Bruevich Saint-Petersburg State University of Telecommunications Publ.; 2018. p.488‒494. (in Russ.) EDN:OVMQXN

38. Wegman M.N., Carter J.L. New Hash Functions and their Use in Authentication and Set Equality. Journal of Computer and System Sciences. 1981;22:265‒279. DOI:10.1016/0022-0000(81)90033-7